Keywords: irt, Rasch, eRm
Prepare data
── Attaching packages ─────────────────────────────────────── tidyverse 1.3.2 ──
✔ ggplot2 3.3.6 ✔ purrr 0.3.4
✔ tibble 3.1.8 ✔ dplyr 1.0.10
✔ tidyr 1.2.0 ✔ stringr 1.4.1
✔ readr 2.1.2 ✔ forcats 0.5.2
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
library (eRm)<- readRDS ("erm_example.rds" )<- dat %>% mutate (sum_d = rowSums (across (starts_with ("D_" ))),sum_a = rowSums (across (starts_with ("A_" )))<- dat %>% select (starts_with ("D_" ))<- dat %>% select (starts_with ("A_" ))
Fit model
<- RM (dat_d)<- RM (dat_a)
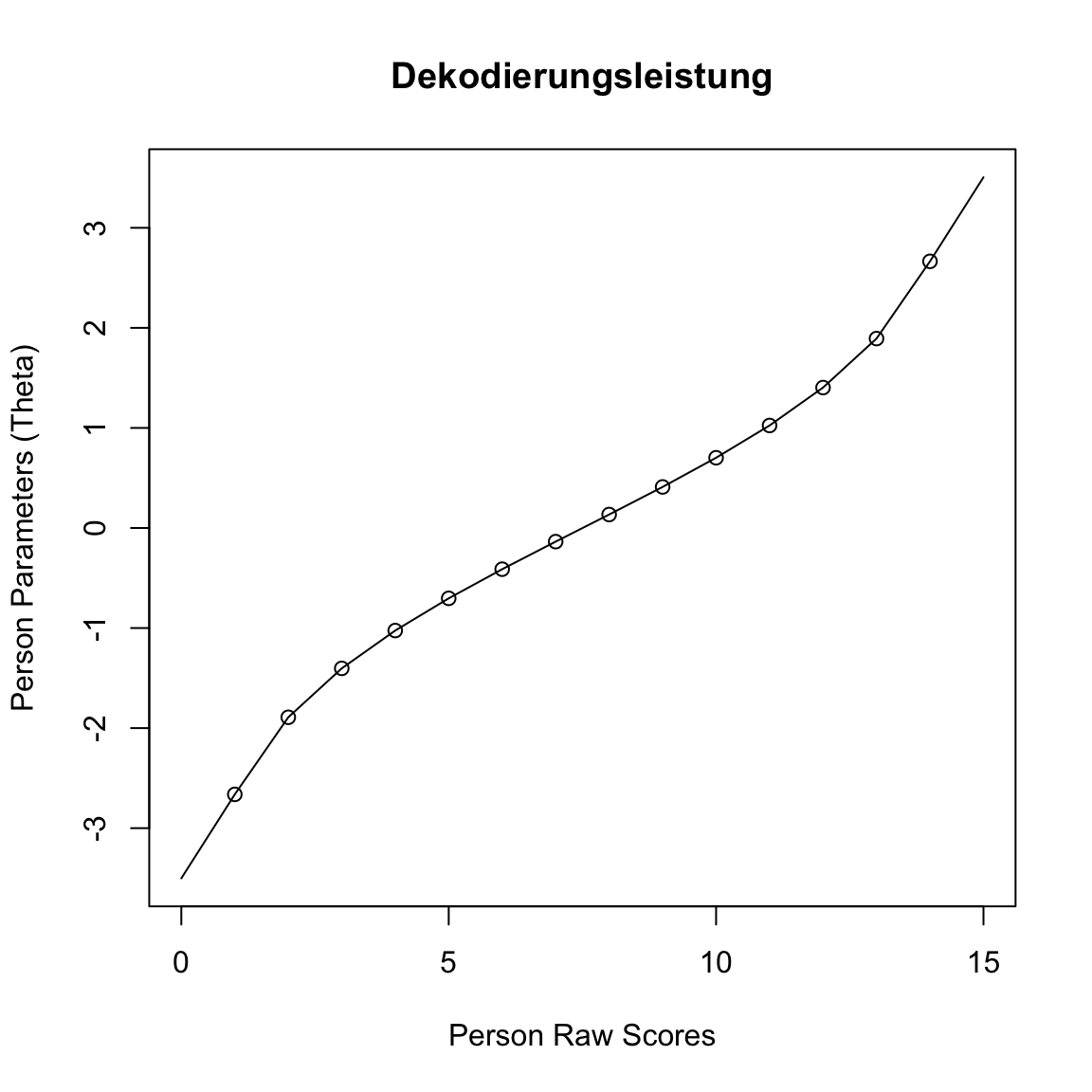
Report item difficulty
Results of RM estimation:
Call: RM(X = dat_d)
Conditional log-likelihood: -290.0775
Number of iterations: 7
Number of parameters: 14
Item (Category) Difficulty Parameters (eta): with 0.95 CI:
Estimate Std. Error lower CI upper CI
D_02_Jan 0.537 0.340 -0.129 1.204
D_03_und -0.064 0.332 -0.716 0.587
D_04_Michael 0.054 0.333 -0.599 0.707
D_05_zum -0.183 0.332 -0.834 0.469
D_06_Schulhof -0.183 0.332 -0.834 0.469
D_07_kommen -0.301 0.333 -0.953 0.351
D_08_stehen 0.054 0.333 -0.599 0.707
D_09_die -0.183 0.332 -0.834 0.469
D_10_meisten 0.293 0.336 -0.364 0.951
D_11_aus 0.414 0.338 -0.247 1.076
D_12_der -0.301 0.333 -0.953 0.351
D_13_Klasse -0.064 0.332 -0.716 0.587
D_14_schon -0.064 0.332 -0.716 0.587
D_15_da 0.054 0.333 -0.599 0.707
Item Easiness Parameters (beta) with 0.95 CI:
Estimate Std. Error lower CI upper CI
beta D_01_Als 0.064 0.332 -0.587 0.716
beta D_02_Jan -0.537 0.340 -1.204 0.129
beta D_03_und 0.064 0.332 -0.587 0.716
beta D_04_Michael -0.054 0.333 -0.707 0.599
beta D_05_zum 0.183 0.332 -0.469 0.834
beta D_06_Schulhof 0.183 0.332 -0.469 0.834
beta D_07_kommen 0.301 0.333 -0.351 0.953
beta D_08_stehen -0.054 0.333 -0.707 0.599
beta D_09_die 0.183 0.332 -0.469 0.834
beta D_10_meisten -0.293 0.336 -0.951 0.364
beta D_11_aus -0.414 0.338 -1.076 0.247
beta D_12_der 0.301 0.333 -0.351 0.953
beta D_13_Klasse 0.064 0.332 -0.587 0.716
beta D_14_schon 0.064 0.332 -0.587 0.716
beta D_15_da -0.054 0.333 -0.707 0.599
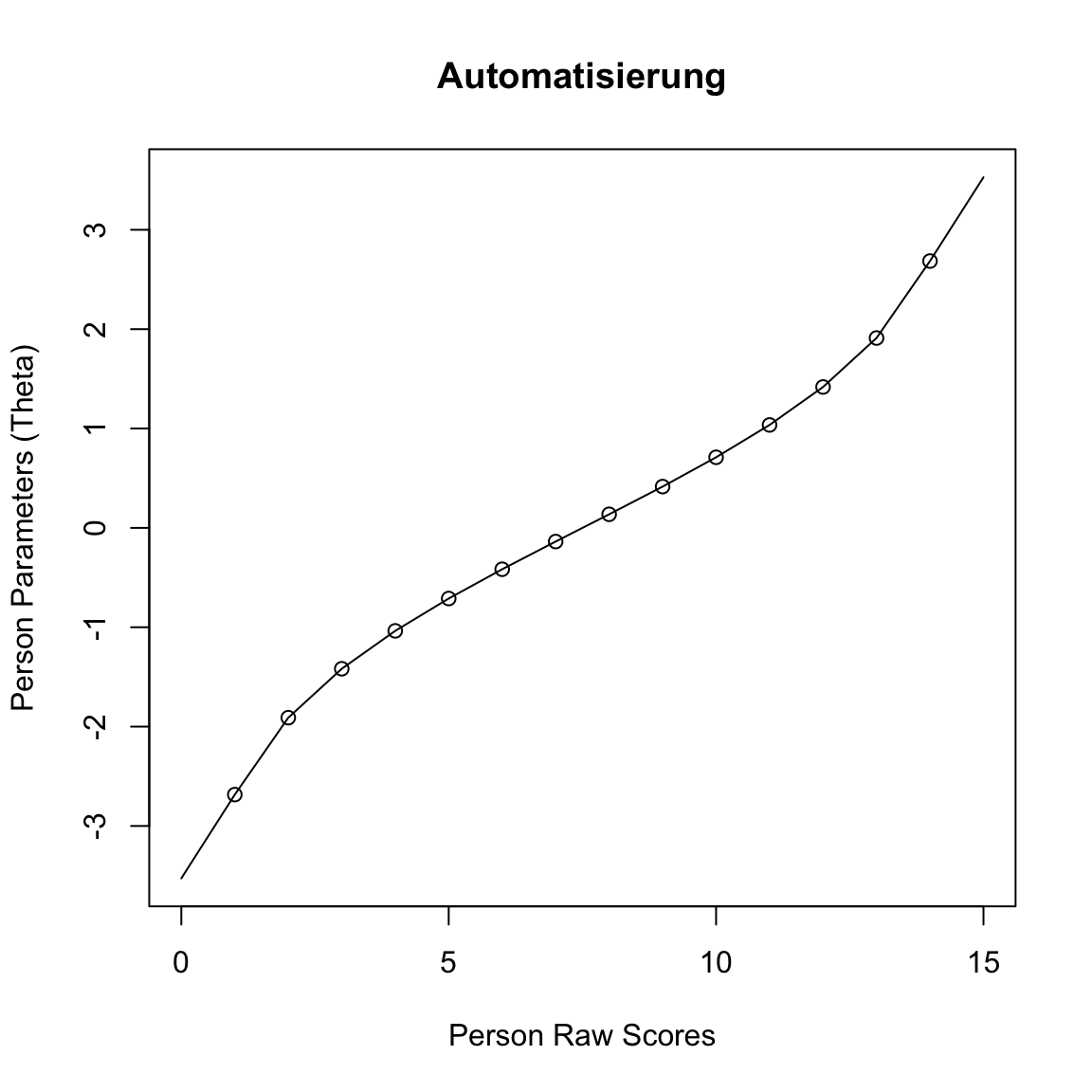
Results of RM estimation:
Call: RM(X = dat_a)
Conditional log-likelihood: -283.8798
Number of iterations: 9
Number of parameters: 14
Item (Category) Difficulty Parameters (eta): with 0.95 CI:
Estimate Std. Error lower CI upper CI
A_02_Jan -0.633 0.342 -1.303 0.037
A_03_und -0.025 0.335 -0.682 0.632
A_04_Michael -0.145 0.335 -0.802 0.513
A_05_zum 0.216 0.336 -0.443 0.876
A_06_Schulhof 0.216 0.336 -0.443 0.876
A_07_kommen -0.025 0.335 -0.682 0.632
A_08_stehen 0.461 0.340 -0.205 1.126
A_09_die 0.096 0.335 -0.562 0.753
A_10_meisten 0.461 0.340 -0.205 1.126
A_11_aus -0.266 0.336 -0.925 0.394
A_12_der 0.585 0.342 -0.086 1.256
A_13_Klasse -0.266 0.336 -0.925 0.394
A_14_schon -0.145 0.335 -0.802 0.513
A_15_da -0.266 0.336 -0.925 0.394
Item Easiness Parameters (beta) with 0.95 CI:
Estimate Std. Error lower CI upper CI
beta A_01_Als 0.266 0.336 -0.394 0.925
beta A_02_Jan 0.633 0.342 -0.037 1.303
beta A_03_und 0.025 0.335 -0.632 0.682
beta A_04_Michael 0.145 0.335 -0.513 0.802
beta A_05_zum -0.216 0.336 -0.876 0.443
beta A_06_Schulhof -0.216 0.336 -0.876 0.443
beta A_07_kommen 0.025 0.335 -0.632 0.682
beta A_08_stehen -0.461 0.340 -1.126 0.205
beta A_09_die -0.096 0.335 -0.753 0.562
beta A_10_meisten -0.461 0.340 -1.126 0.205
beta A_11_aus 0.266 0.336 -0.394 0.925
beta A_12_der -0.585 0.342 -1.256 0.086
beta A_13_Klasse 0.266 0.336 -0.394 0.925
beta A_14_schon 0.145 0.335 -0.513 0.802
beta A_15_da 0.266 0.336 -0.394 0.925
Test Modelfit
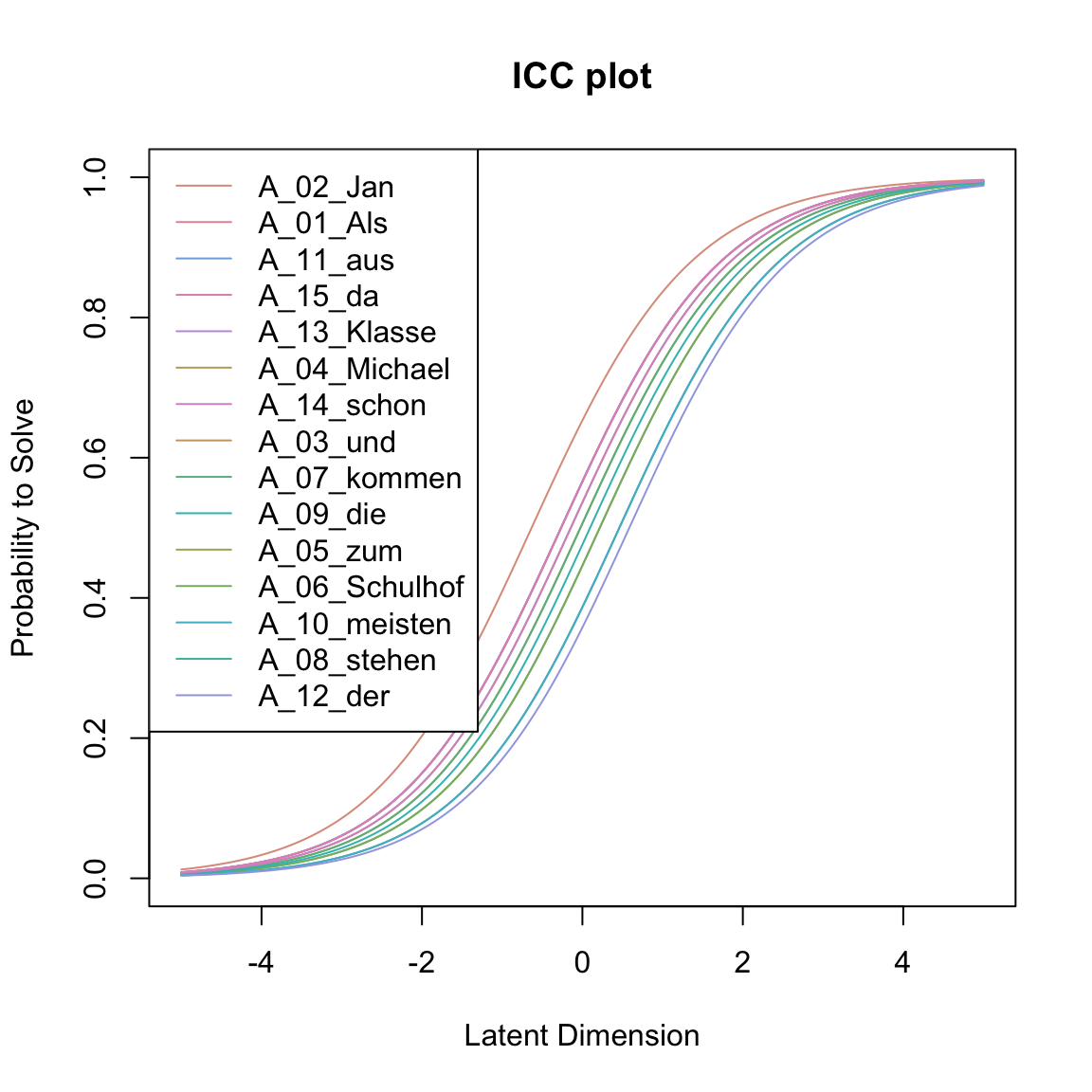
Visual inspection of item discrimination
plotjointICC (fit_d, xlim = c (- 5 , 5 ))plotjointICC (fit_a, xlim = c (- 5 , 5 ))
Likelihood ratio tests
LRtests test for the estimation “stability” across several sub-samples of the data set.
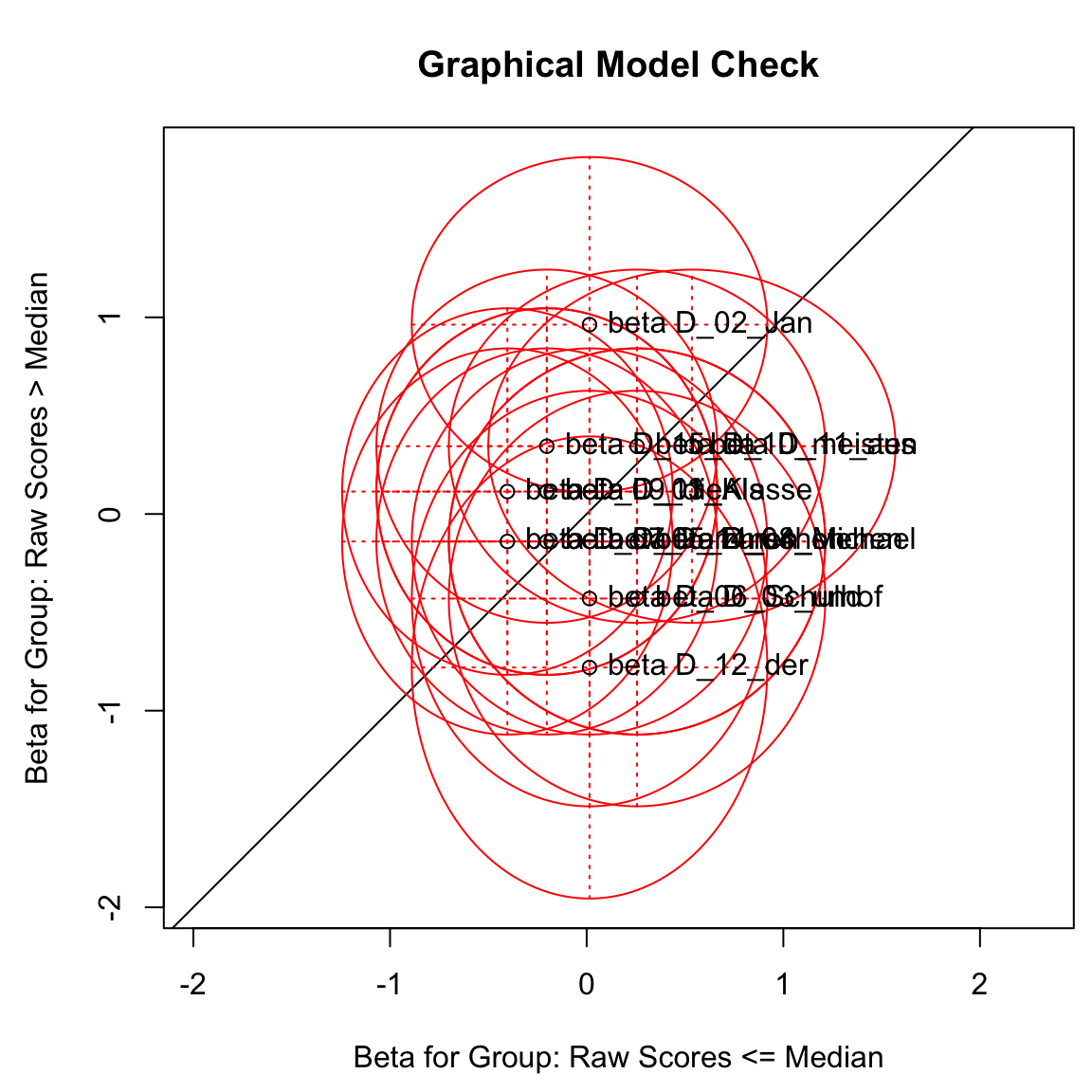
A median split allows for checking if the item-difficulty estimations are constant for the lower and upper part of the performance scale. This is similar to a test for homoscedasticity.
<- LRtest (fit_d, splitcr = "median" )<- LRtest (fit_a, splitcr = "median" )
Andersen LR-test:
LR-value: 6.954
Chi-square df: 14
p-value: 0.936
Andersen LR-test:
LR-value: 17.088
Chi-square df: 14
p-value: 0.252
plotGOF (lr_d, conf= list ())plotGOF (lr_a, ctrline= list ())
Wald Test
Wald test on item level (z-values):
z-statistic p-value
beta D_01_Als 0.488 0.626
beta D_02_Jan 1.496 0.135
beta D_03_und -0.943 0.346
beta D_04_Michael -0.566 0.572
beta D_05_zum 0.094 0.925
beta D_06_Schulhof -0.626 0.531
beta D_07_kommen 0.400 0.689
beta D_08_stehen -0.566 0.572
beta D_09_die 0.808 0.419
beta D_10_meisten 0.132 0.895
beta D_11_aus -0.272 0.785
beta D_12_der -1.051 0.293
beta D_13_Klasse 0.488 0.626
beta D_14_schon -0.227 0.821
beta D_15_da 0.860 0.390
Wald test on item level (z-values):
z-statistic p-value
beta A_01_Als -0.336 0.737
beta A_02_Jan -0.239 0.811
beta A_03_und 1.184 0.236
beta A_04_Michael -0.648 0.517
beta A_05_zum 1.894 0.058
beta A_06_Schulhof 1.195 0.232
beta A_07_kommen -2.341 0.019
beta A_08_stehen -0.311 0.756
beta A_09_die -0.598 0.550
beta A_10_meisten -0.311 0.756
beta A_11_aus -0.336 0.737
beta A_12_der 0.000 1.000
beta A_13_Klasse -0.336 0.737
beta A_14_schon 0.803 0.422
beta A_15_da 1.827 0.068
Item In-Fit / Out Fit
ItemFit interpretation:
larger 2.0: Distorts or degrades the measurementsystem
1.5-2.0: Unproductive for construction of measurement, but not degrading
0.5-1.5: Productive for measurement
<0.5: Lessproductive for measurement, but not degrading. May produce misleadingly good reliabilities and separations
Itemfit Statistics:
Chisq df p-value Outfit MSQ Infit MSQ Outfit t Infit t Discrim
D_01_Als 60.546 44 0.049 1.345 1.212 1.276 1.287 0.360
D_02_Jan 55.231 44 0.119 1.227 1.163 0.846 0.950 0.397
D_03_und 26.844 44 0.981 0.597 0.731 -1.722 -1.791 0.713
D_04_Michael 42.051 44 0.555 0.934 0.931 -0.171 -0.382 0.569
D_05_zum 46.485 44 0.370 1.033 1.029 0.211 0.232 0.490
D_06_Schulhof 43.466 44 0.494 0.966 0.988 -0.040 -0.021 0.527
D_07_kommen 45.764 44 0.399 1.017 1.036 0.153 0.277 0.462
D_08_stehen 38.572 44 0.703 0.857 0.932 -0.491 -0.375 0.558
D_09_die 52.715 44 0.173 1.171 1.064 0.697 0.444 0.457
D_10_meisten 36.926 44 0.766 0.821 0.907 -0.634 -0.515 0.571
D_11_aus 33.483 44 0.876 0.744 0.815 -0.945 -1.106 0.637
D_12_der 33.313 44 0.880 0.740 0.892 -0.947 -0.652 0.569
D_13_Klasse 57.032 44 0.090 1.267 1.124 1.027 0.792 0.417
D_14_schon 47.227 44 0.342 1.049 0.937 0.273 -0.344 0.560
D_15_da 57.058 44 0.090 1.268 1.174 1.036 1.068 0.382
Itemfit Statistics:
Chisq df p-value Outfit MSQ Infit MSQ Outfit t Infit t Discrim
A_01_Als 63.799 45 0.034 1.387 1.123 1.244 0.785 0.432
A_02_Jan 44.536 45 0.491 0.968 1.006 0.018 0.090 0.544
A_03_und 49.213 45 0.308 1.070 1.164 0.330 1.037 0.427
A_04_Michael 35.200 45 0.853 0.765 0.889 -0.765 -0.672 0.601
A_05_zum 62.154 45 0.046 1.351 1.290 1.163 1.735 0.334
A_06_Schulhof 40.073 45 0.680 0.871 1.017 -0.354 0.157 0.534
A_07_kommen 22.361 45 0.998 0.486 0.640 -2.086 -2.575 0.783
A_08_stehen 28.876 45 0.970 0.628 0.823 -1.268 -1.104 0.655
A_09_die 41.513 45 0.620 0.902 0.878 -0.245 -0.759 0.625
A_10_meisten 40.687 45 0.655 0.885 0.899 -0.278 -0.584 0.589
A_11_aus 34.902 45 0.861 0.759 0.929 -0.772 -0.395 0.591
A_12_der 39.471 45 0.705 0.858 0.891 -0.347 -0.621 0.582
A_13_Klasse 33.062 45 0.906 0.719 0.884 -0.933 -0.693 0.610
A_14_schon 51.039 45 0.248 1.110 1.110 0.456 0.718 0.470
A_15_da 103.787 45 0.000 2.256 1.387 3.192 2.191 0.239
Person In-Fit / Out Fit
Personfit interpretation:
larger 2.0: Distorts or degrades the measurementsystem
1.5-2.0: Unproductive for construction of measurement, but not degrading
0.5-1.5: Productive for measurement
<0.5: Lessproductive for measurement, but not degrading. May produce misleadingly good reliabilities and separations
Personfit Statistics:
Chisq df p-value Outfit MSQ Infit MSQ Outfit t Infit t
P3 18.927 14 0.168 1.262 1.049 0.61 0.27
P5 15.238 14 0.362 1.016 1.015 0.22 0.21
P6 14.437 14 0.418 0.962 1.000 0.27 0.30
P7 13.111 14 0.518 0.874 0.945 -0.19 -0.02
P8 15.300 14 0.358 1.020 1.012 0.17 0.13
P9 13.724 14 0.470 0.915 0.982 0.04 0.15
P10 14.481 14 0.415 0.965 0.991 -0.03 0.06
P11 17.025 14 0.255 1.135 1.058 0.55 0.30
P12 15.999 14 0.313 1.067 1.043 0.39 0.29
P13 18.603 14 0.181 1.240 1.098 0.69 0.37
P14 14.437 14 0.418 0.962 1.000 0.27 0.30
P15 13.724 14 0.470 0.915 0.982 0.04 0.15
P16 15.778 14 0.327 1.052 1.035 0.27 0.22
P17 13.620 14 0.478 0.908 0.960 -0.10 0.02
P18 15.606 14 0.338 1.040 1.041 0.59 0.59
P19 13.829 14 0.463 0.922 0.957 -0.18 -0.07
P20 15.778 14 0.327 1.052 1.035 0.27 0.22
P21 13.658 14 0.475 0.911 0.936 -0.40 -0.29
P22 13.922 14 0.456 0.928 0.926 -1.01 -1.05
P23 13.165 14 0.514 0.878 0.880 -1.77 -1.76
P24 13.396 14 0.496 0.893 0.919 -0.49 -0.39
P25 14.991 14 0.379 0.999 1.000 0.02 0.03
P26 13.170 14 0.513 0.878 0.880 -1.77 -1.76
P27 15.468 14 0.347 1.031 1.021 0.29 0.22
P28 16.349 14 0.293 1.090 1.067 0.74 0.60
P29 14.214 14 0.434 0.948 0.953 -0.72 -0.68
P30 16.024 14 0.312 1.068 1.063 0.95 0.93
P31 15.018 14 0.377 1.001 1.007 0.07 0.10
P32 14.503 14 0.413 0.967 0.975 -0.02 0.00
P33 14.440 14 0.417 0.963 0.968 -0.26 -0.23
P34 17.361 14 0.237 1.157 1.109 0.62 0.47
P35 14.218 14 0.434 0.948 0.955 -0.20 -0.18
P36 14.667 14 0.401 0.978 0.973 0.08 0.06
P37 13.428 14 0.493 0.895 0.966 0.00 0.12
P38 15.561 14 0.341 1.037 1.014 0.25 0.14
P39 14.890 14 0.386 0.993 0.985 0.03 -0.02
P40 17.319 14 0.240 1.155 1.049 0.45 0.27
P41 16.305 14 0.295 1.087 1.036 0.34 0.25
P42 14.612 14 0.405 0.974 1.005 0.28 0.30
P43 9.352 14 0.808 0.623 0.923 -0.16 0.21
P44 15.099 14 0.371 1.007 1.021 0.15 0.18
P45 15.065 14 0.374 1.004 1.005 0.09 0.09
P46 16.332 14 0.294 1.089 1.020 0.40 0.32
P47 16.305 14 0.295 1.087 1.036 0.34 0.25
P48 18.262 14 0.195 1.217 1.034 0.53 0.34
Personfit Statistics:
Chisq df p-value Outfit MSQ Infit MSQ Outfit t Infit t
P4 12.220 14 0.589 0.815 0.980 0.11 0.27
P5 8.725 14 0.848 0.582 0.911 -0.21 0.19
P6 14.450 14 0.417 0.963 1.011 0.14 0.20
P7 16.258 14 0.298 1.084 0.981 0.34 0.15
P8 13.671 14 0.475 0.911 0.999 0.22 0.30
P9 13.088 14 0.520 0.873 0.937 -0.34 -0.15
P10 8.725 14 0.848 0.582 0.911 -0.21 0.19
P11 14.977 14 0.380 0.998 0.996 0.01 -0.02
P12 14.291 14 0.428 0.953 1.000 0.02 0.13
P13 16.408 14 0.289 1.094 1.082 0.50 0.48
P14 16.279 14 0.297 1.085 1.040 0.34 0.26
P15 12.310 14 0.581 0.821 0.957 -0.12 0.10
P16 19.363 14 0.152 1.291 1.057 0.65 0.29
P17 18.928 14 0.168 1.262 1.122 0.72 0.43
P18 12.792 14 0.543 0.853 0.867 -1.06 -1.04
P19 15.592 14 0.339 1.039 1.022 0.26 0.22
P20 14.411 14 0.420 0.961 0.988 -0.12 0.00
P21 12.136 14 0.595 0.809 0.814 -2.18 -2.21
P22 14.732 14 0.397 0.982 0.980 -0.16 -0.20
P23 13.039 14 0.523 0.869 0.884 -0.93 -0.89
P24 14.846 14 0.389 0.990 0.995 -0.08 -0.02
P25 13.750 14 0.468 0.917 0.909 -0.90 -1.02
P26 16.428 14 0.288 1.095 1.096 1.03 1.08
P27 13.448 14 0.492 0.897 0.899 -1.13 -1.16
P28 15.995 14 0.314 1.066 1.070 0.38 0.42
P29 13.976 14 0.451 0.932 0.940 -0.45 -0.43
P30 16.719 14 0.271 1.115 1.111 1.22 1.25
P31 17.110 14 0.250 1.141 1.117 1.01 0.90
P32 16.487 14 0.285 1.099 1.094 1.07 1.07
P33 12.345 14 0.579 0.823 0.845 -0.83 -0.78
P34 13.757 14 0.468 0.917 0.921 -0.56 -0.58
P35 17.053 14 0.253 1.137 1.119 0.99 0.92
P36 15.893 14 0.320 1.060 1.063 0.66 0.73
P37 15.219 14 0.363 1.015 1.031 0.15 0.20
P38 14.328 14 0.426 0.955 1.007 0.27 0.30
P39 15.560 14 0.341 1.037 1.048 0.22 0.26
P40 15.269 14 0.360 1.018 1.014 0.15 0.14
P41 14.119 14 0.441 0.941 0.951 -0.10 -0.09
P42 13.641 14 0.477 0.909 0.965 -0.09 0.04
P43 17.825 14 0.215 1.188 1.071 0.50 0.31
P44 12.803 14 0.542 0.854 0.989 0.15 0.28
P45 20.151 14 0.125 1.343 1.050 0.64 0.35
P46 20.151 14 0.125 1.343 1.050 0.64 0.35
P47 11.101 14 0.678 0.740 0.910 -0.29 0.02
P48 20.151 14 0.125 1.343 1.050 0.64 0.35
P49 20.152 14 0.125 1.343 1.050 0.64 0.35