Skip to contents

Randomization Tests for single-case data

Source: R/rand_test.R
rand_test.Rd

The rand_test function computes a randomization test for single or multiple baseline single-case data. The function is based on an algorithm from the SCRT package (Bulte & Onghena, 2009, 2012), but rewritten and extended for the use in AB designs.

Usage

rand_test(
  data,
  dvar,
  pvar,
  statistic = c("Mean B-A", "Mean A-B", "Median B-A", "Median A-B", "Mean |A-B|",
    "Median |A-B|", "SMD hedges", "SMD glass", "W-test", "T-test", "NAP",
    "NAP decreasing", "Slope B-A", "Slope A-B"),
  statistic_function = NULL,
  number = 500,
  complete = FALSE,
  limit = 5,
  startpoints = NA,
  exclude.equal = FALSE,
  phases = c(1, 2),
  graph = FALSE,
  output = NULL,
  seed = NULL
)

Arguments

data

A single-case data frame. See scdf() to learn about this format.

dvar

Character string with the name of the dependent variable. Defaults to the attributes in the scdf file.

pvar

Character string with the name of the phase variable. Defaults to the attributes in the scdf file.

statistic

Defines the statistic on which the comparison of phases A and B is based on. Default setting is statistic = "Mean B-A". See details.

statistic_function

A list with a user defined function to calculate the statistic. When set, overwrites the statistic argument. See details.

number

Sample size of the randomization distribution. The exactness of the p-value can not exceed \(1/number\) (i.e., number = 100 results in p-values with an exactness of one percent). Default is number = 500. For faster processing use number = 100. For more precise p-values set number = 1000).

complete

If TRUE, the distribution is based on a complete permutation of all possible starting combinations. This setting overwrites the number Argument. The default setting is FALSE.

limit

Minimal number of data points per phase in the sample. The first number refers to the A-phase and the second to the B-phase (e.g., limit = c(5,3)). If only one number is given, this number is applied to both phases. Default is limit = 5.

startpoints

Alternative to the limit-parameter startpoints exactly defines the possible start points of phase B (e.g., startpoints = 4:9 restricts the phase B start points to measurements 4 to 9. startpoints overruns the limit-parameter.

exclude.equal

If set to exclude.equal = FALSE, which is the default, random distribution values equal to the observed distribution are counted as null-hypothesis conform. That is, they decrease the probability of rejecting the null-hypothesis (increase the p-value). exclude.equal should be set to TRUE if you analyse one single-case design (not a multiple baseline data set) to reach a sufficient power. But be aware, that it increases the chance of an alpha-error.

phases

A vector of two characters or numbers indicating the two phases that should be compared. E.g., phases = c("A","C") or phases = c(2,4) for comparing the second to the fourth phase. Phases could be combined by providing a list with two elements. E.g., phases = list(A = c(1,3), B = c(2,4)) will compare phases 1 and 3 (as A) against 2 and 4 (as B). Default is phases = c(1,2).

graph

If graph = TRUE, a histogram of the resulting distribution is plotted. It is FALSE by default. Note: use the more versatile plot_rand() function instead.

output

(deprecated and not implemented)

seed

A seed number for the random generator.

Value

statistic

Character string from function call (see Arguments above).

N

Number of single-cases.

n1

Number of data points in phase A.

n2

Number of data points in phase B.

limit

Numeric from function call (see Arguments above).

startpoints

A vector defining the start points passed from the function call (see Arguments above).

p.value

P-value of the randomization test for the given data.

number

Sample size of randomization distribution from function call (see Arguments above).

complete

Logical argument from function call (see Arguments above).

observed.statistic

Test statistic observed for the given single-case data. (see statistic in the Arguments above.)

Z

Z-value of observed test statistic.

p.z.single

Probability of z-value.

distribution

Test statistic distribution from randomized data sets.

possible.combinations

Number of possible combinations under the given restrictions.

auto.corrected.number

TRUE indicates that a corrected number of combinations was used. This happens, if the number of possible combinations (under the given restrictions) undercuts the requested number of combinations.

ecxlude.equal

see argument above

Details

Predefinded statisic

Use the statistic argument to choose a predefnied statistic. The following comparisons are possible:

  • Mean A-B: Uses the difference between the mean of phase A and the mean of phase B. This is appropriate if a decrease of scores was expected for phase B.

  • Mean B-A: Uses the difference between the mean of phase B and the mean of phase A. This is appropriate if an increase of scores was expected for phase B.

  • Mean |A-B|: Uses the absolute value of the difference between the means of phases A and B.

  • Median A-B: The same as Mean A-B, but based on the median.

  • Median B-A: The same as Mean B-A, but based on the median.

  • SMD hedges / SMD glass: Standardizes mean difference of B-A as Hedges's g or Glass' delta.

  • NAP: Non-overlap of all pairs.

  • W-test: Wilcoxon-test statistic W.

  • T-test: T-test statistic t.

Create own statistic function

Use the statistic_function argument to proved your own function in a list. This list must have an element named statistic with a function that takes two arguments a and b and returns a single numeric value. E.g. list(statistic = function(a, b) mean(a) - mean(b). A second element of the list is named aggregate which takes a function with one numeric argument that returns a numeric argument. This function is used to aggregate the values of a multiple case design. If you do not provide this element, it uses the default function(x) sum(x)/length(x). The third optional argument is name which provides a name for your user function.

References

Bulte, I., & Onghena, P. (2009). Randomization tests for multiple-baseline designs: An extension of the SCRT-R package. Behavior Research Methods, 41, 477-485.

Bulte, I., & Onghena, P. (2012). SCRT: Single-Case Randomization Tests. Available from: https://CRAN.R-project.org/package=SCRT

Author

Juergen Wilbert

Examples


## Compute a randomization test on the first case of the byHeart2011 data and include a graph
rand_test(byHeart2011[1], statistic = "Median B-A", graph = TRUE, seed = 123)

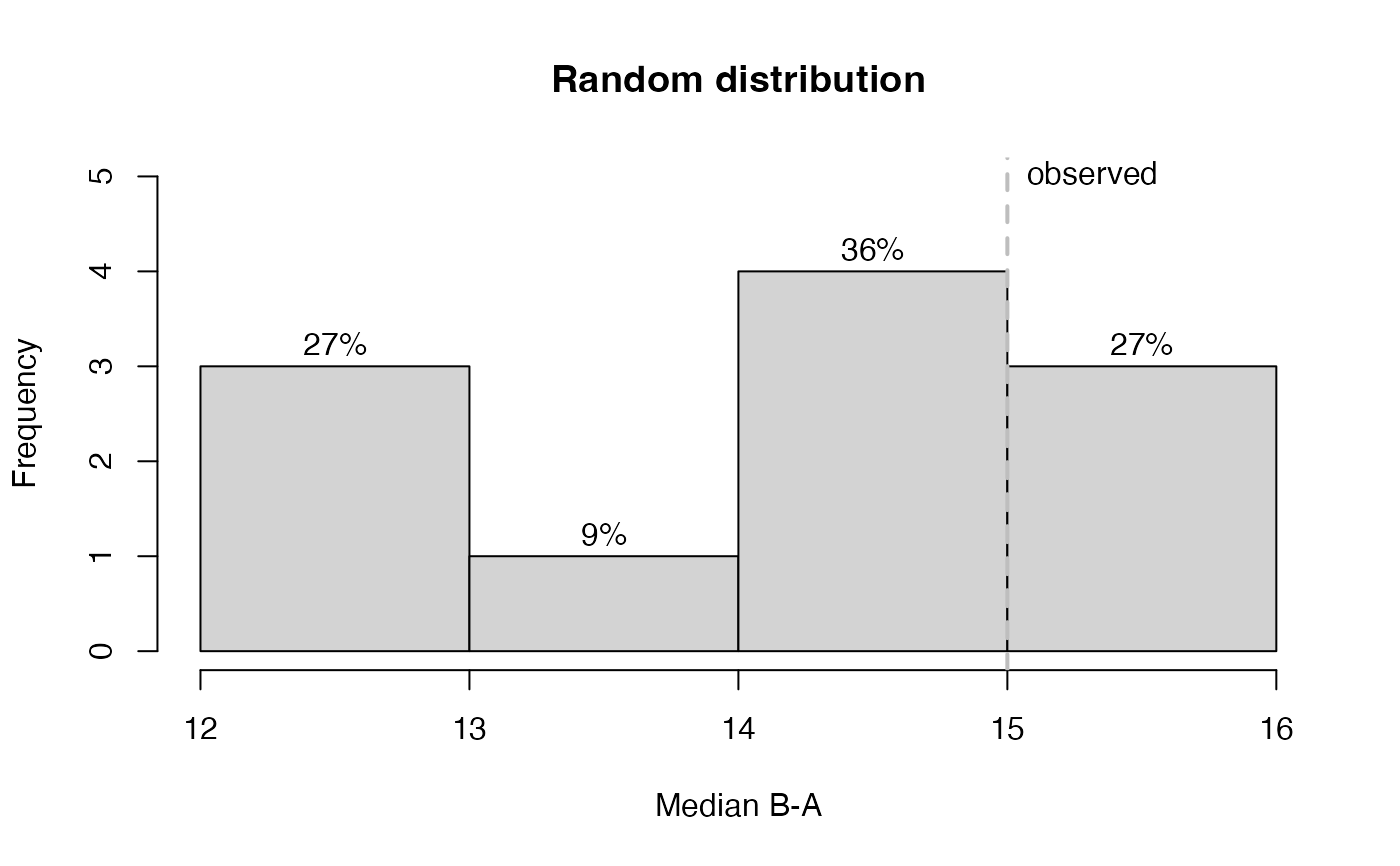#> Randomization Test
#> 
#> Comparing phase 1 against phase 2 
#> Statistic:  Median B-A 
#> 
#> Minimal length of each phase: A = 5 , B = 5 
#> Observed statistic =  15 
#> 
#> Warning! The assigned number of random permutations exceeds the number of possible permutations. 
#> Analysis is restricted to all possible permutations.
#> 
#> Distribution based on all 11 possible combinations.
#> n   =  11 
#> M   =  14.40909 
#> SD  =  1.338249 
#> Min =  12 
#> Max =  16 
#> 
#> Probability of an equal or higher value than the observed statistic:
#> p   =  0.6363636 
#> 
#> Shapiro-Wilk Normality Test: W = 0.868; p = 0.073  (Hypothesis of normality maintained)
#> 
#> Probabilty of observed statistic based on the assumption of normality:
#> z = 0.4416, p = 0.3294 (single sided)

## Compute a randomization test on the Grosche2011 data using complete permutation
rand_test(Grosche2011, statistic = "Median B-A", complete = TRUE, limit = 4, seed = 123)
#> Randomization Test
#> 
#> Combined test for three cases.
#> 
#> Comparing phase 1 against phase 2 
#> Statistic:  Median B-A 
#> 
#> Minimal length of each phase: A = 4 , B = 4 
#> Observed statistic =  0.365 
#> 
#> Distribution based on all 2652 possible combinations.
#> n   =  2652 
#> M   =  1.004859 
#> SD  =  0.7805234 
#> Min =  -1.445 
#> Max =  1.71 
#> 
#> Probability of an equal or higher value than the observed statistic:
#> p   =  0.8435143 
#> 
#> Shapiro-Wilk Normality Test: W = 0.804; p = 0.000  (Hypothesis of normality rejected)
#> 
#> Probabilty of observed statistic based on the assumption of normality:
#> z = -0.8198, p = 0.7938 (single sided)